函数过程调用

对于一个过程 (函数 / 方法)，必须要支持下面一个或多个机制：

传递控制：自动更新程序计数器 PC 的值
传递数据：提供参数传递和结果返回功能
分配和释放内存：提供内存的分配和释放机制

传递控制

在传递控制部分，我们需要做的事情是自动更新程序计数器 PC 的值，让程序能够按照正确的顺序执行。要做到自动更新 PC 的值，我们需要做到下面两点：

调用过程前将返回地址压栈，以便被调过程返回时能够继续执行。同时将 PC 的值设置为被调函数的首地址值，以便程序能够执行被调函数
被调函数返回时，将返回地址弹栈，并将 PC 的值设置为这个返回地址，以便程序能从调用位置够继续执行
在 x86-64 中，分别使用 call 指令和 ret 指令来实现这两个功能。

数据传递

在过程的调用过程中，后调用的过程一般会先执行完毕，所有程序一般都会使用栈作为数据结构来管理内存。一个过程可能会有许多信息，这部分信息也需要存储在栈上，这一部分称之为栈帧。一个通用栈帧示意图如下图所示。

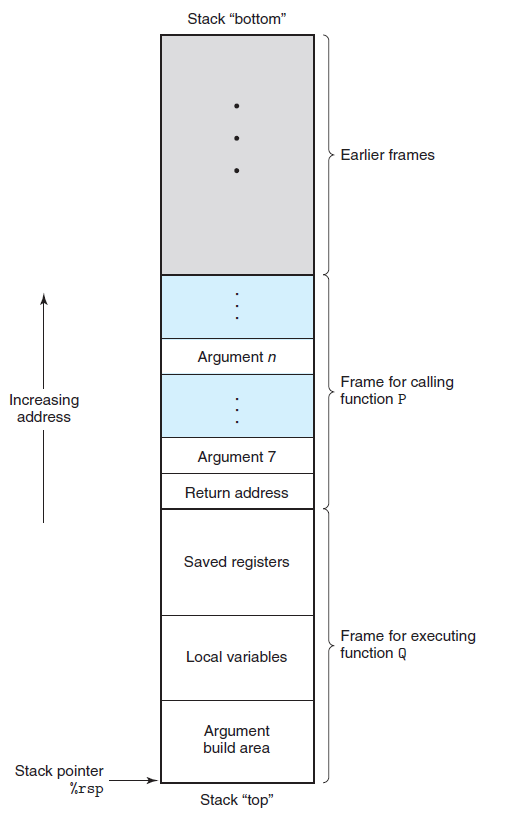
参数传递

在 x86-64 中，可以通过寄存器最多传递 6 个整型参数，而这些寄存器是有顺序。过程中传递的参数依次存放到寄存器 %rdi、%rsi、%rdx、%rcx、%r8、%r9 中。如果一个函数有大于 6 个整型参数，超出 6 个的部分需要通过栈来传递，并且这些数据大小都需要向 8 的倍数对齐。如果在过程中调用了某个超过了 6 个参数的函数，则需要在栈帧中为超过 6 个部分的参数分配过程，这一部分称之为 “参数构造区”。
对于下面的程序，函数 proc 接受 8 个参数，包括字节数不同的整数和不同类型的指针。

void proc(long  a1, long    *a1p,
        int     a2, int     *a2p,
        short   a3, short   *a3p,
        char    a4, char    *a4p) {
    *a1p += a1;
    *a2p += a2;
    *a3p += a3;
    *a4p += a4;
}

我们查看汇编代码（原始的、为被优化的代码，并且只保留了重要部分）

proc:
.LFB0:
	movq	16(%rsp), %rax	; 将 a4 放入 %rax 中
	addq	%rdi, (%rsi)	; *a1p += a1
	addl	%edx, (%rcx)	; *a2p += a2
	addw	%r8w, (%r9)	; *a3p += a3
	movl	8(%rsp), %edx	; 将 a4 存放到 %edx 中
	addb	%dl, (%rax)	; *a4p += a4
	ret

从汇编代码中可以看出，参数 a1, *a1p, a2, *a2p, a3, *a3p 分别存放在寄存器 %rdi、%rsi、%rdx、%rcx、%r8、%r9 中。而我们通过 8(%rsp) 和 16(%rsp) 分别访问了 a4 和 *a4，并且我们发现这两个参数在栈中是逆序存储的。由此可以证明，过程的前 6 个整型参数是通过寄存器传递的，而超过 6 个的部分是通过栈来存储的。

在 x86-32 中没有使用寄存器来传递参数，所有参数都需要在栈上分配。可以通过 -m32 来指定编译为 32 位机器上的代码，然后查看汇编代码来验证。也可以通过这篇博客了解

既然参数会使用寄存器存储，而且通用寄存器是公用的，那么如果我们在被调用函数中改变了寄存器中的值会影响参数原本的值吗。根据我们的经验，值传递是不会改变变量原来的值的。那么程序是如何做到这一点的呢？
要想保证值不被其他函数修改，只有两种方法

在调用函数前保存一份，函数返回后恢复，这种方式被称为调用者保存
在被调函数中保存，返回前恢复，这种方式被称为被调用者保存
在 x86 中，通用寄存器被划分为调用者保存和被调用者保存两类，其中寄存器 %rbx、%rbp 和 %r12~%15 是被调用者保存，其他寄存器位调用者保存。在需要保存寄存器中的值的时候，这些值也是保存在栈上的。

局部变量存储

对于过程中的局部变量，有些可以直接使用寄存器存取，但是有些变量需要存储在栈上，常见的情况包括：

寄存器不足够存放所有的本地数据
对一个局部变量使用取地址运算符 &，这时不能能够为它产生一个地址
某些局部变量数组或结构

数组分配和访问

在 C 语言中，数组是一种将标量数据聚集程更大数据类型的方式，也就是说数组中的元素是分配在一块连续的内存空间中的。
对于数据类型 T ，有一维数组 T A[N]; ，假设数组首地址为 $X_{A}$ ，则数组中第 i 个元素存放在 $X_{A} + L \cdot i$ 中（L 为数据类型 T 的大小）。如果有二维数组 T A[M][N]，则数组元素 $A[i][j]$ 计算地址的方式为 $X_{A} + L (N \cdot i + j)$ 。也就是说数组元素是按照 “行优先” 的顺序存放的。